01背包

有一个背包容量为 $V$，还有 $n$ 件物品，第 $i$ 件的体积为 $v[i]$，价值为 $w[i]$，问背包能装载的最大价值

先站在背包的角度想一想

原背包 （偷懒，画背包太难了，画成袋子算了）。

这么大个背包，装啥好呢？

先想一想，背包是不是有分很多格？

那我们也来分一分

分成2个子背包。

子背包还能再分。

再站在物品的角度想一想

2种情况：装、不装。

如果装，那背包余剩的容量就会减少。

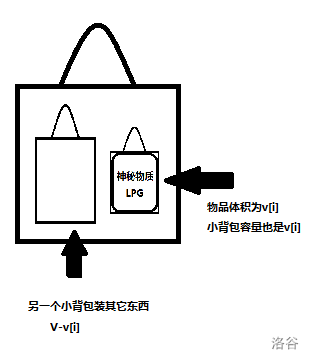
这么说的话，是用记忆化搜索吗？

NO！NO！NO！我们要 DP。

上代码

1
2
3
4
5
6
7
8
9
int dp[N][V]; //dp[i][j]表示在考虑了前i种物品、背包容量为j的情况下的最大装载价值
for (int i = 1; i <= n; i++) { //遍历每种物品
	for (int j = 1; j <= V; j++) { //递推背包容量
		if (j >= v[i]) //如果能装得下物品i
			dp[i][j] = max(dp[i - 1][j], //不装物品i
				dp[i - 1][j - v[i]] + w[i]; //装物品i
		else dp[i][j] = dp[i - 1][j]; // 装不下，直接不装
	}
}

优化

首先我们想想能不能把 dp 数组压缩成1维。

好，现在如果你去试了，那么恭喜你，发现了错误。

那如果你没去试的话，那么也恭喜你，没被我坑。

出错原因

看下这行代码

1
dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - v[i]] + w[i]);

$j-v[i]$ 是不是在前面它已经更新过了，更新过意味着可能已经装过物品 $i$ 了，所以可能导致重复装入。

解决办法

如果它已经更新过了，就可能会出错。

那就先别更新呗！先更新后面的，把第二层循环倒过来。

1
2
3
4
5
6
7
8
9
int dp[V]; //dp[j]表示当前背包容量为j时的最大装载价值
for (int i = 1; i <= n; i++) { //遍历每种物品
	for (int j = V; j >= 1; j--) { //递推背包容量（倒过来）
		if (j >= v[i]) //如果能装得下物品i
			dp[j] = max(dp[j], //不装物品i
				dp[j - v[i]] + w[i]; //装物品i
//		else dp[j] = dp[j]; //没用的语句
   }
}

删掉if语句

由于第二层循环到 $v[i]-1$ 时，物品已经装不下了，所以我们就不用继续循环了，dp数组剩下的部分就放着（不装）。

1
2
3
4
5
int dp[V]; //dp[j]表示当前背包容量为j时的最大装载价值
for (int i = 1; i <= n; i++) //遍历每种物品
	for (int j = V; j >= v[i]; j--) //递推背包容量（倒过来）
		dp[j] = max(dp[j], //不装物品i
			dp[j - v[i]] + w[i]; //装物品i

算法复杂度分析：

  • 时间复杂度：二重循环，$O(nV)$。

  • 空间复杂度：一维dp数组，$O(V)$。

完全背包

在01背包上加点花样，每种物品都有无限个。

我们先来看一个很眼熟的东西:

$j-v[i]$ 是不是在前面它已经更新过了，更新过意味着可能已经装过物品i了，所以可能导致重复装入

是的，你曾经在这儿被我坑过一次。

重复装入 意味着物品i可以不受限制地选下去，就相当于物品i有无限个。

1
2
3
4
5
int dp[V]; //dp[j]表示当前背包容量为j时的最大装载价值
for (int i = 1; i <= n; i++) //遍历每种物品
	for (int j = v[i]; j <= V; j++) //递推背包容量
		dp[j] = max(dp[j], //不装物品i
			dp[j - v[i]] + w[i]; //装物品i

算法复杂度分析：

  • 时间复杂度：二重循环，$O(nV)$

  • 空间复杂度：一维dp数组，$O(V)$

多重背包

还是在01背包上加点花样，每种物品都有 $m[i]$ 个。

1
2
3
4
5
for (int i = 1; i <= n; i++)
	for (int j = V; i >= v[i]; i--)
		for (int k = 1; k <= min(m[i], j / v[i]); k++)
			dp[j] = max(dp[j], dp[j - v[i] * k] + w[i] * k);

算法复杂度分析：

  • 时间复杂度：三重循环，$O(nVm)$

  • 空间复杂度：一维dp数组，$O(V)$